7. 합성곱 신경망

25 Nov 2020

합성곱 신경망인 Convolutional Neural Network(CNN)은 이미지 인식 음성인식 등 다양한 분야에서 사용되는데, 특히 이미지 인식 분야에서 자주 사용된다.

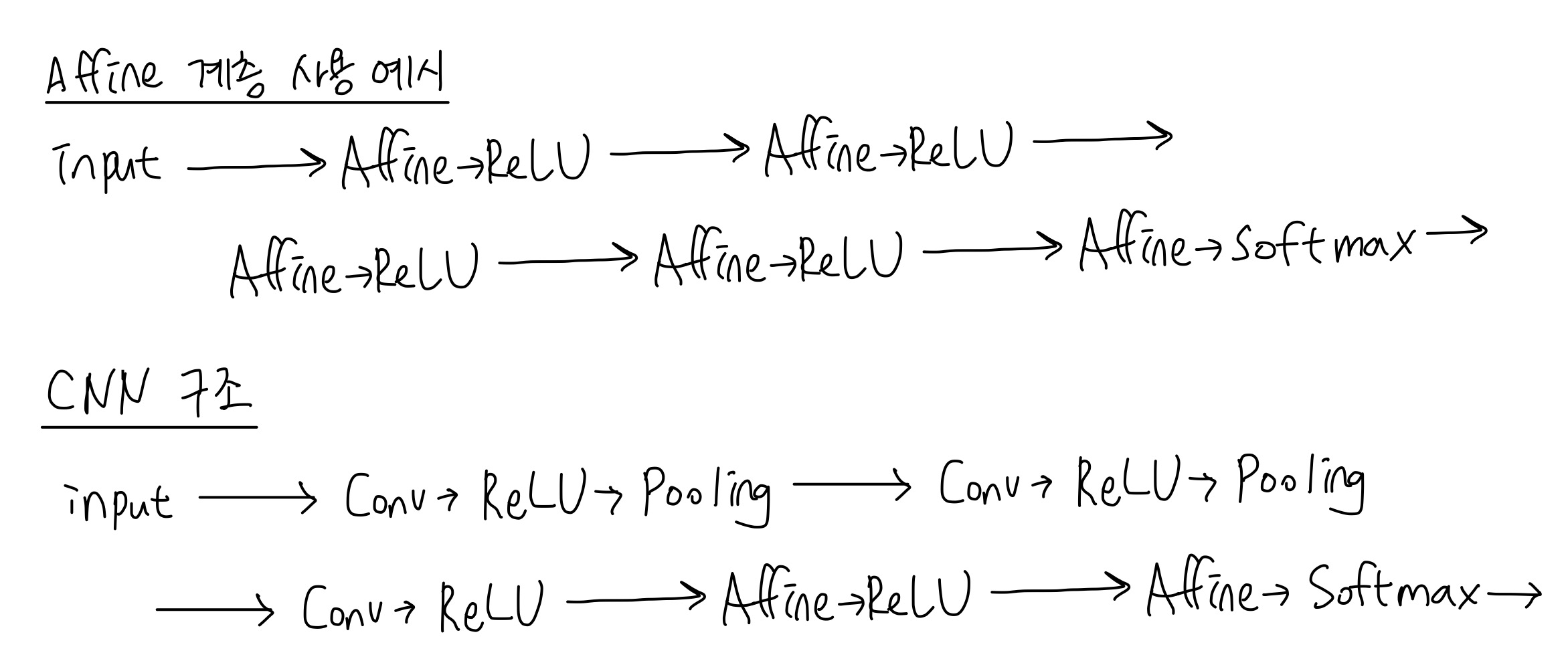
기존의 완전 연결 계층인 Affine 계층에 추가적으로 합성곱 신경망은 합성곱 계층(Convolutional layer), 그리고 풀링 계층(Pooling layer)을 사용한다.

합성곱 계층

합성곱 신경망에서도 출력 가까이에서는 Affine 계층을 사용한다.

완전연결계층을 사용하면 3차원 데이터를 그대로 사용하지 못하고 1차원으로 펴줘야 한다. 이전에 MNIST를 Affine 계층으로 학습시켰을 때를 생각해보면 28x28인 이미지를 1x784 배열로 바꿔서 사용하였다.

합성곱 신경망에서는 이러한 입력값의 형상을 유지한 채로 연산을 할 수 있는데, 합성곱 계층의 입출력 데이터를 특징맵이라고 부른다. (입력특징맵, 출력특징맵)

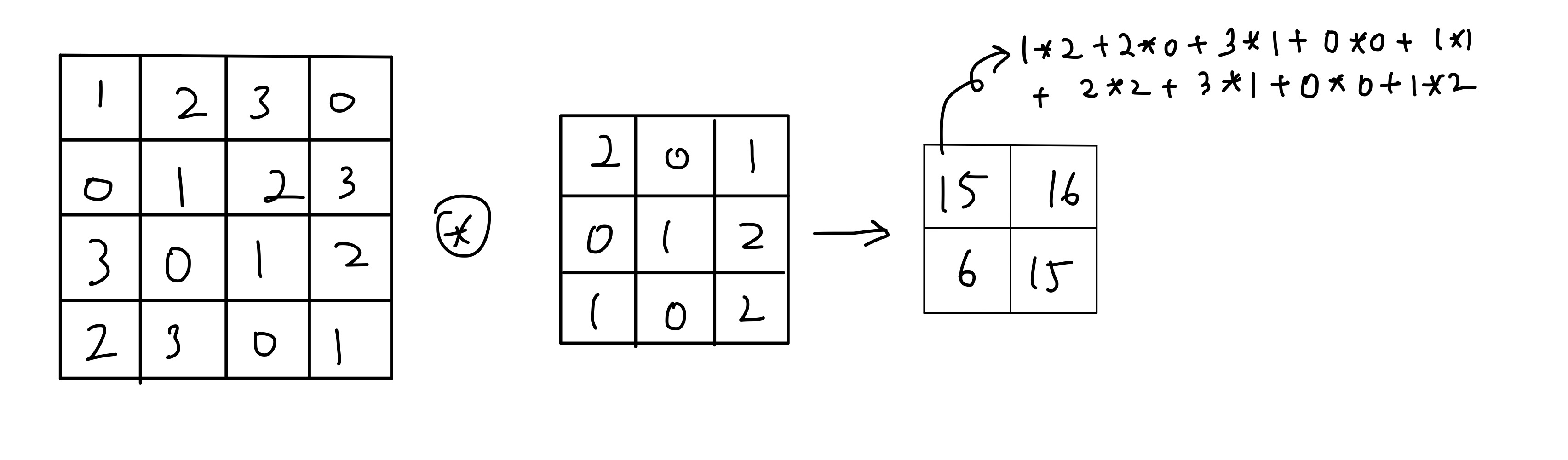
합성곱 연산의 예시는 다음과 같다.

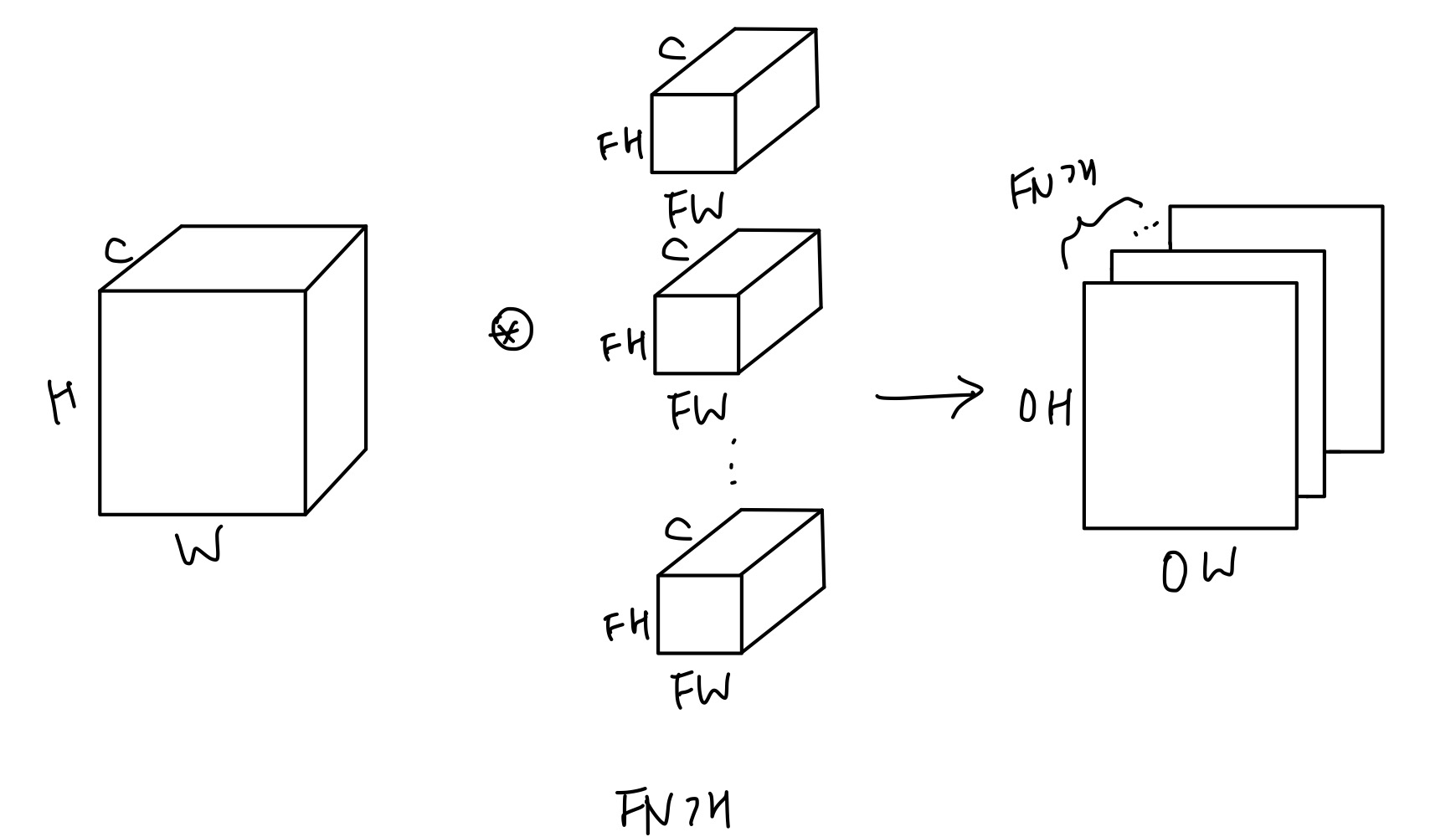
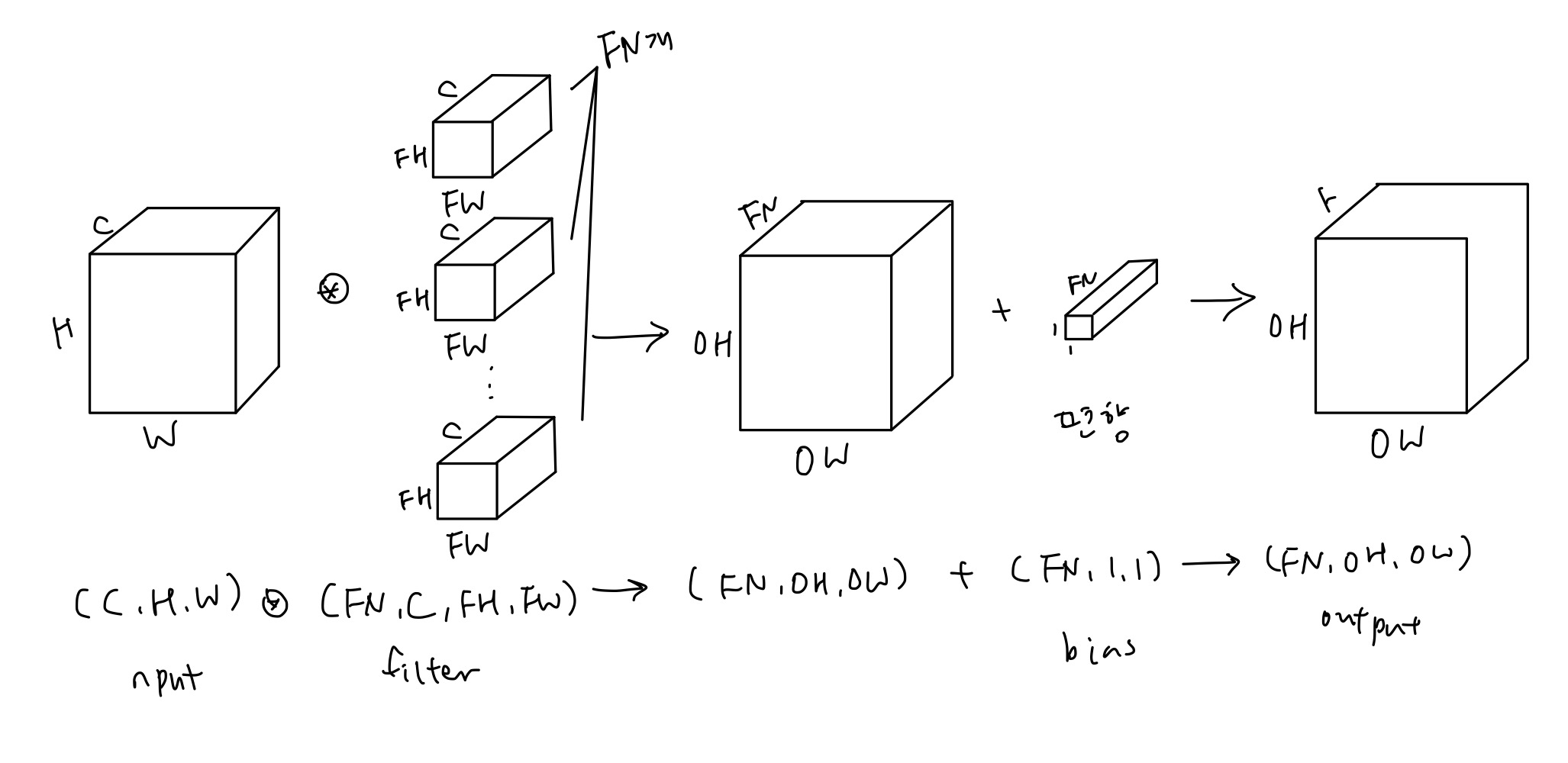
합성곱 연산은 필터의 윈도우를 일정 간격으로 이동해가면서 입력 데이터에 적용을 하는 방식인데, 단일곱셈-누산이라고 입력과 필터에서 대응되는 원소끼리 곱한 값들의 총 합을 구한다. 이 때 필터의 매개변수가 가중치의 역할을 하고, 편향은 필터연산 후에 더해준다. 편향은 하나의 값을 필터를 적용한(출력의) 모든 원소에 더해준다.

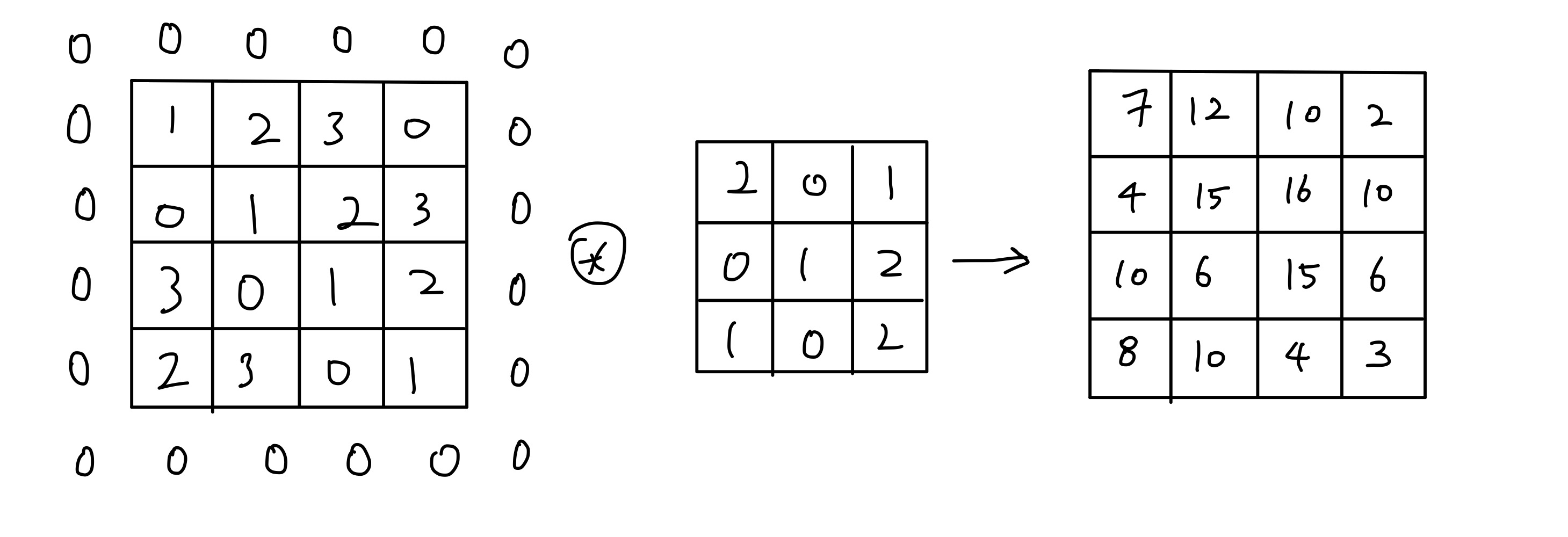
패딩도 해줄 수 있다.

패딩은 출력의 크기를 조정하는데에 사용된다.

합성곱 연산을 하면 할 수록 출력이 점점 작아지다가 1x1까지 작아질 수 있다. 이러한 일을 방지하기 위해 패딩을 해서 입력과 출력의 크기를 동일하게 해줄 수 있다.

스트라이드는 필터가 이동하는 간격이다. 스트라이드가 커지면 출력이 작아진다.

지금까지 살펴본 입력, 필터, 패딩, 스트라이드를 가지고 출력의 형상을 아래와 같이 계산할 수 있다.

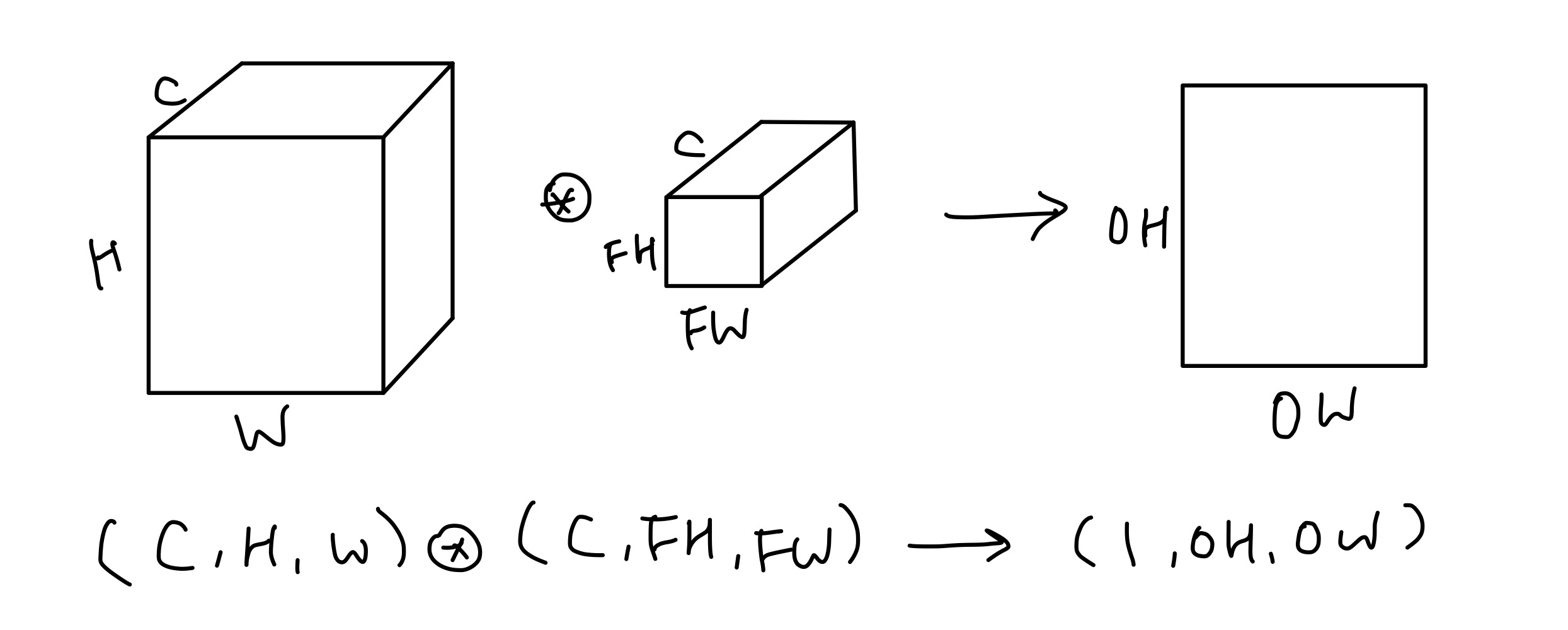
지금까지의 예시는 2차원 데이터였는데, 3차원 데이터에 대해서는 어떻게 연산을 할까?

입력 데이터와 필터의 합성곱 연산을 채널마다 수행하고 결과를 더해 하나의 출력값으로 만들어주는데, 이 때 입력 데이터의 채널 수와 필터의 채널 수가 같아야 하고, 각 채널별 필터의 크기가 같아야 한다.

위 그림을 보면 출력 데이터가 채널이 1인 특징맵이다. 그렇다면 출력이 여러 채널로 나오게 하려면 어떻게 해야 하는가? 필터를 여러개 두면 된다.

참고로 편향을 더해준 경우는 다음과 같다.

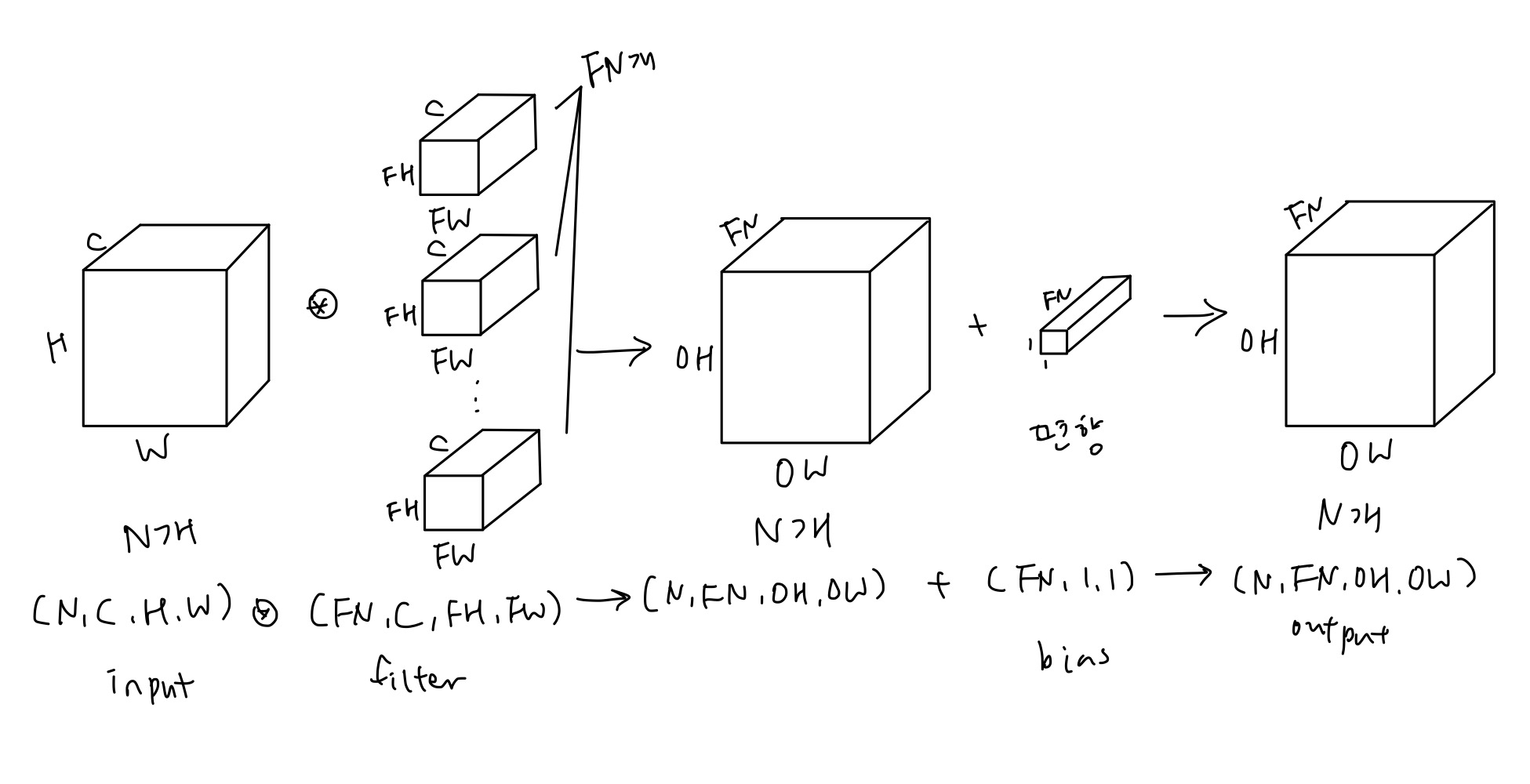
이를 배치로 처리하려면 어떻게 하는가? 데이터의 차원을 하나 늘린다.

풀링 계층

풀링은 가로 세로 방향의 공간을 줄이는 연산이다.

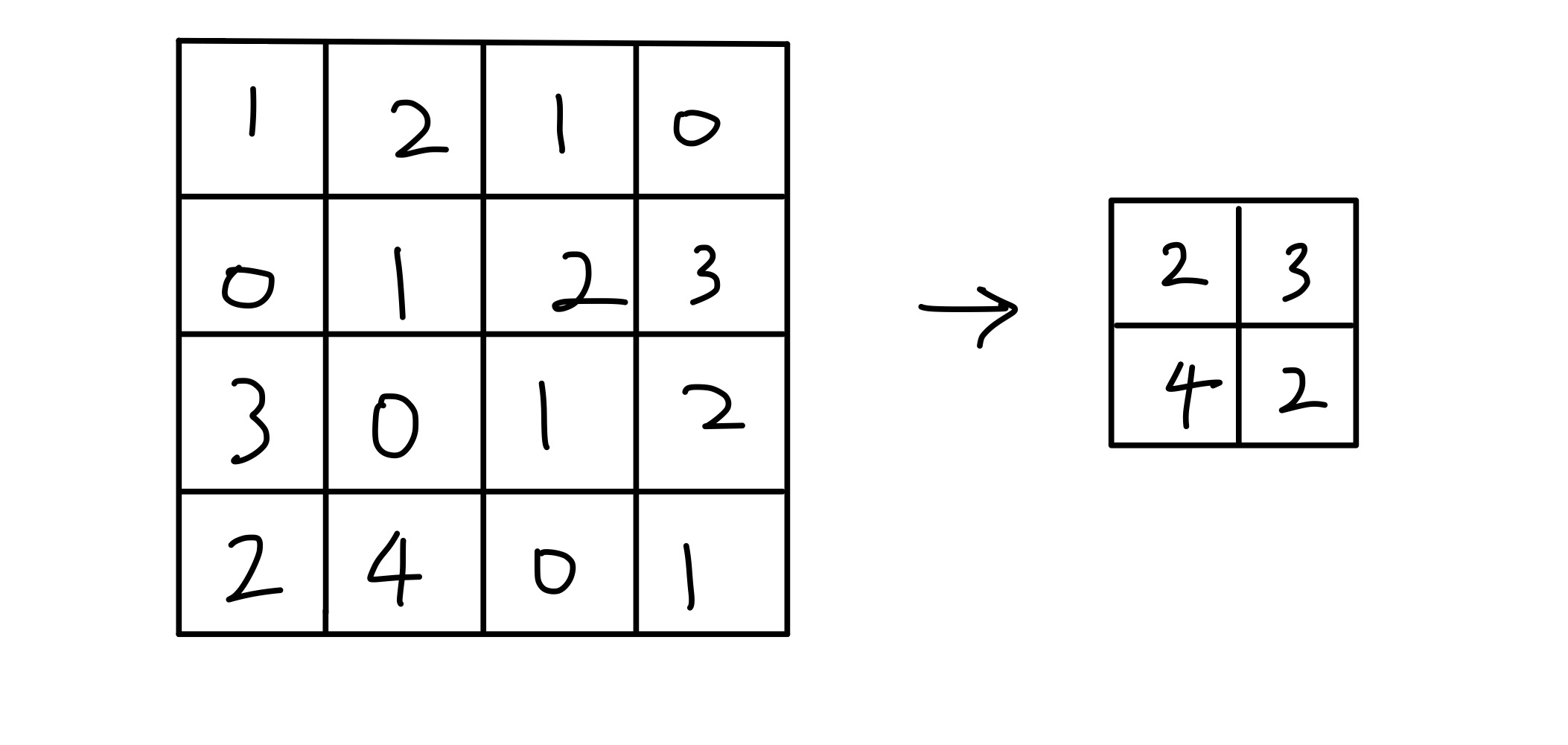
예를 들어 2x2 최대 풀링은 다음과 같다.

풀링 윈도우 크기와 스트라이드는 보통 동일하게 둔다고 한다.

풀링 계층의 특징은 학습이 필요한 매개변수가 없고, 채널 수가 변하지 않고, 입력의 변화에 큰 영향을 받지 않는다는 것이다.

합성곱 신경망의 구현은 오른쪽 링크에서 확인할 수 있다. -> link

CNN은 계층을 깊이 쌓을 수록 더 복잡하고 추상화된 정보를 추출할 수 있다.

대표적인 CNN 모델로는 LeNet과 AlexNet이 있다.

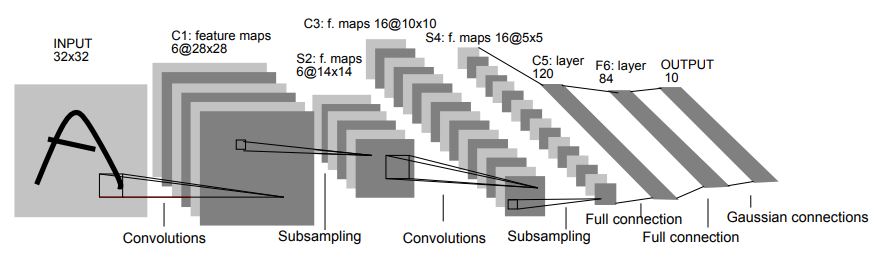
LeNet은 CNN의 원조라고 볼 수 있는 모델로 활성화함수로 시그모이드를 사용한다.

AlexNet은 합성곱 계층과 풀링 계층을 거듭해서 마지막으로 완전연결 계층을 거치는데 활성화 함수로 ReLU를 사용하고 Local Response Normalization(LRM)이라는 국소적 정규화를 실시하고, 드롭아웃을 사용한다.

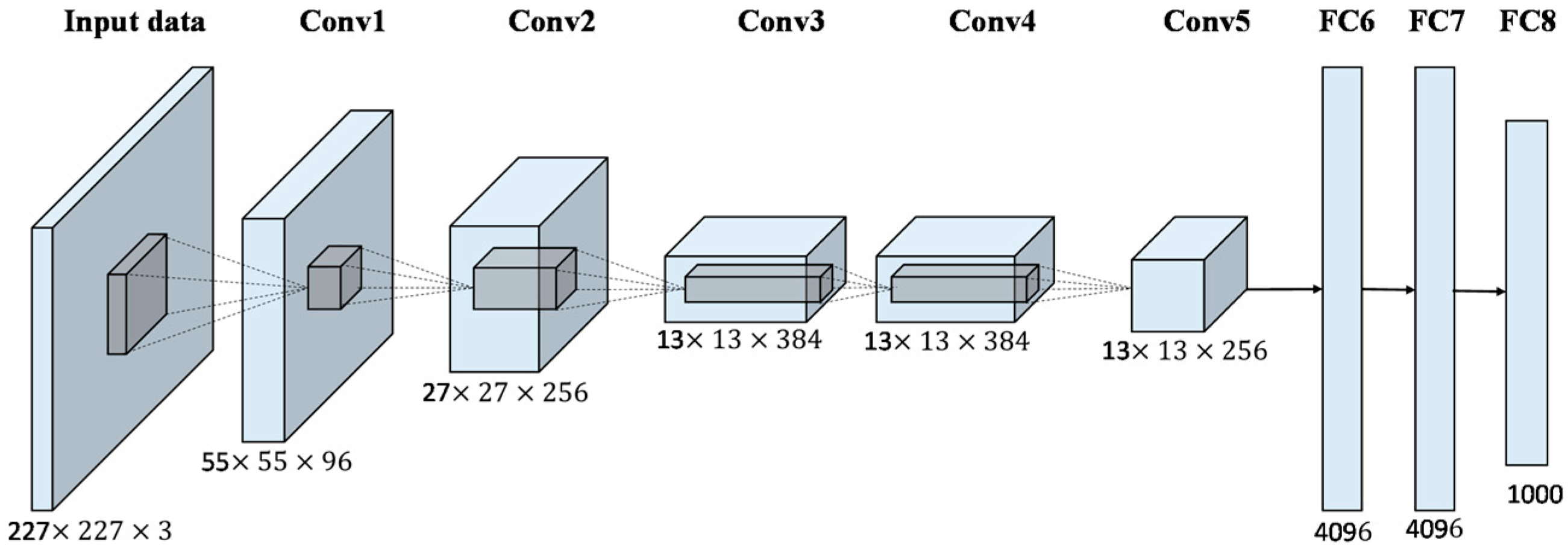
사실상 빅데이터와 GPU의 보급으로 성능이 좋아졌다고 볼 수 있다.