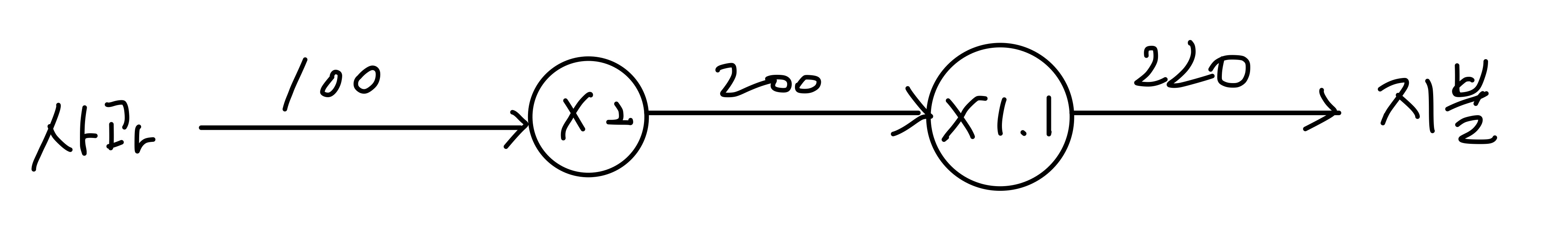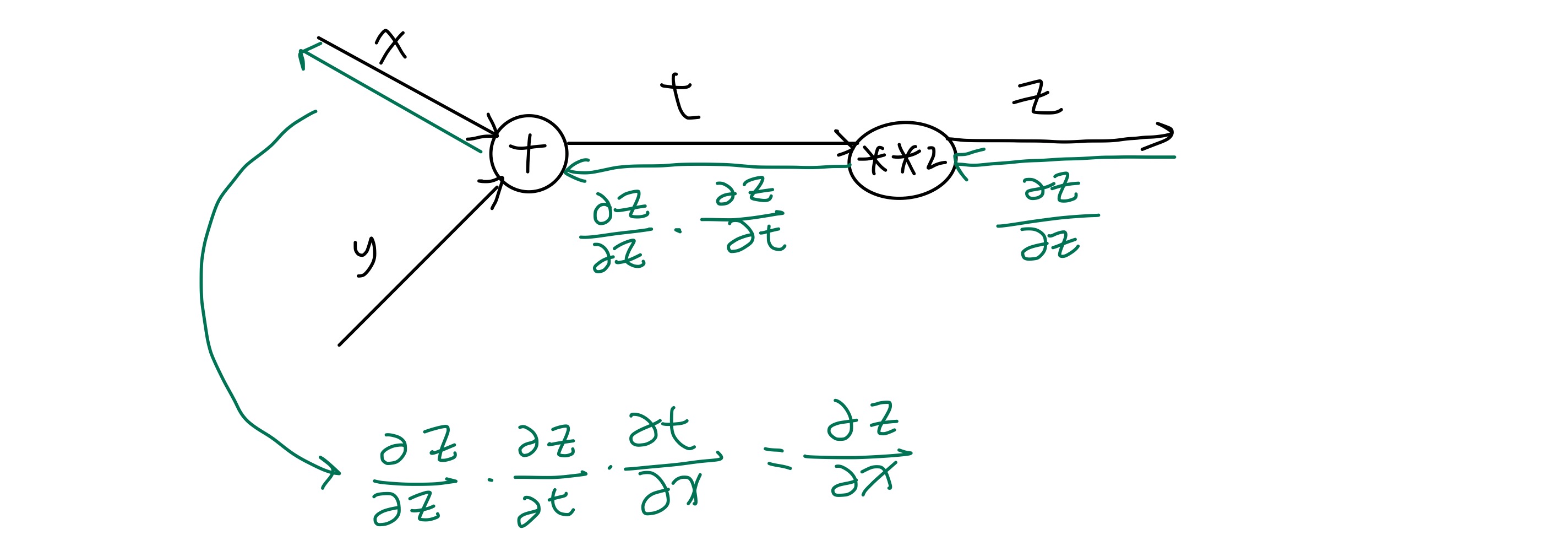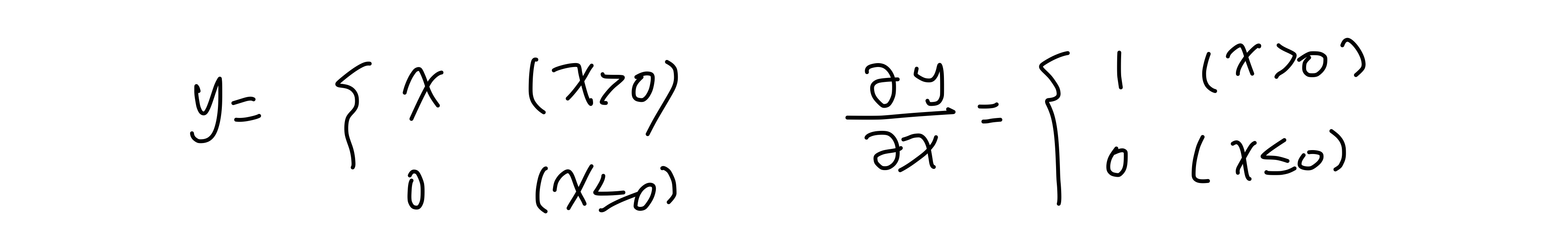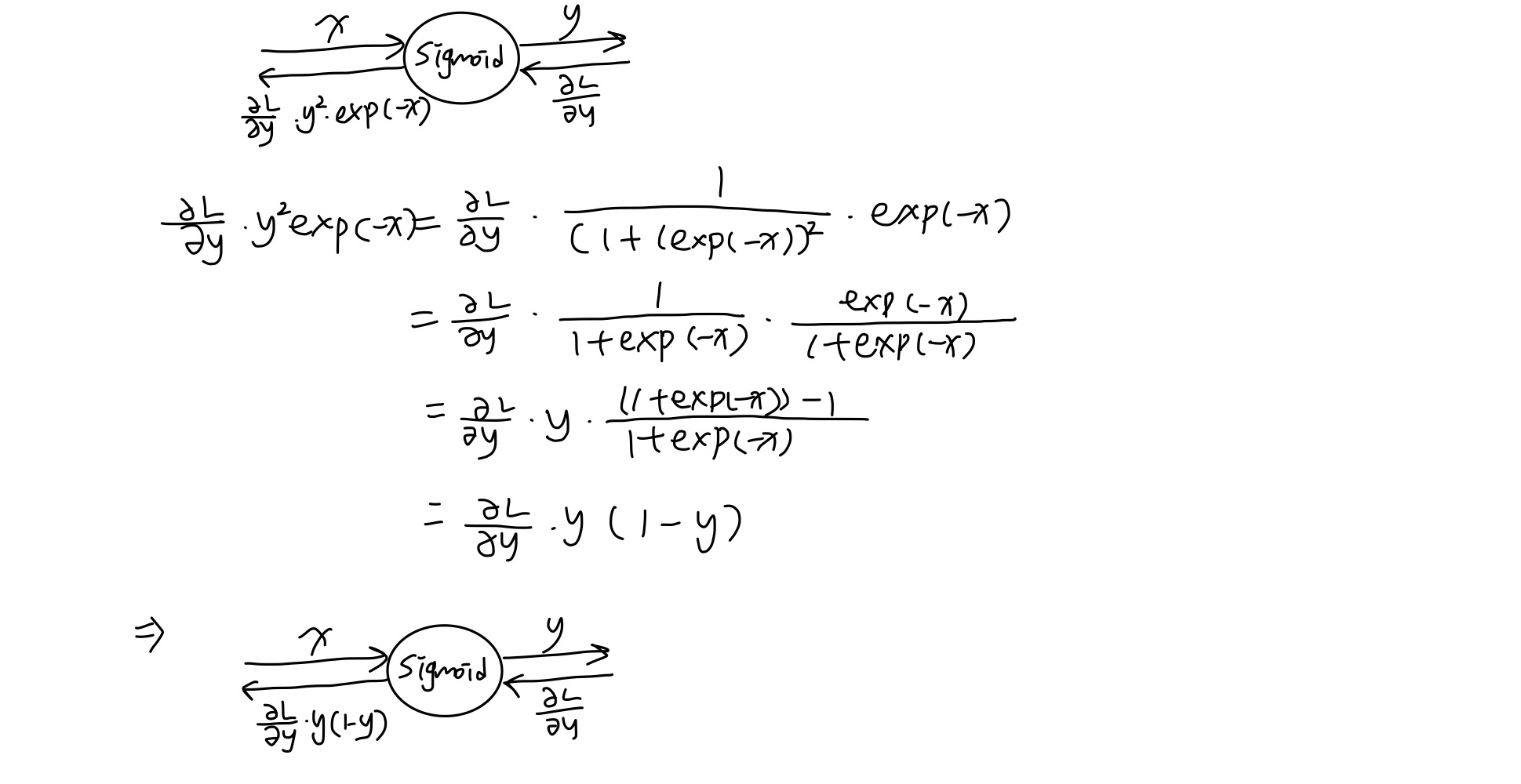5. 오차역전파법
20 Nov 2020앞 챕터에서 봤듯이 신경망의 가중치 매개변수 기울기는 수치 미분을 사용해서 구할 수 있다. 미분을 사용하는 방법은 단순하고 구현이 쉽지만 계산이 오래 걸린다.
가중치 매개변수를 효율적으로 계산하는 방법으로는 오차 역전파법이 있다. 오차 역전파법을 이해하는 방법에는 크게 수식을 사용하는 방법과 그래프를 사용하는 방법이 있는데, 해당 저자는 그래프, 그 중에서 계산 그래프를 사용하였다. 이 때문에 해당 챕터 설명에는 사진을 많이 첨부할 것이고 종종 설명 또한 사진에 첨부할 것이다.
계산 그래프
소비세가 10%일 때 100원짜리 사과를 2개를 사기 위한 값을 계산하는 과정을 아래 계산 그래프와 같이 나타낼 수 있다.
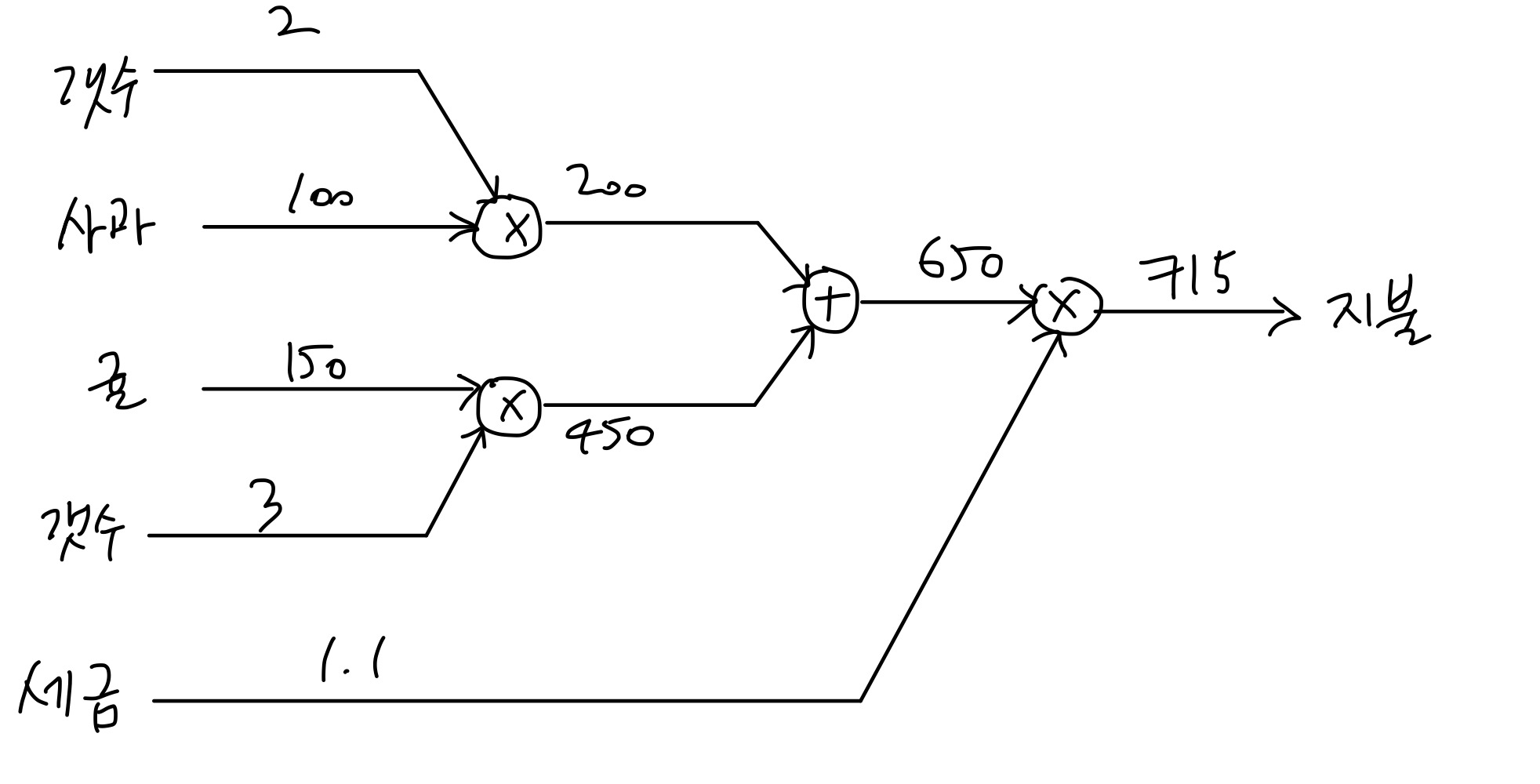
같은 원리로 소비세가 10%일 때 100원짜리 사과 2개와 150원짜리 귤 3개를 사기 위한 값을 계산하는 과정은 아래 계산 그래프와 같이 나타낼 수 있다.
정리해보면, 계산 그래프를 이용한 문제풀이 단계는 다음과 같다.
- 계산 그래프를 구성한다.
- 그래프의 계산을 왼쪽에서 오른쪽으로 진행한다. 이렇게 왼쪽에서 오른쪽으로 진행되는 계산은 순전파라고 하고, 반대로 오른쪽에서 왼쪽으로 전파하는 방법은 역전파라고 한다.
계산그래프의 장점은 자신과 관련된 작은 범위만 고려하면 된다는 것인데, 예를 들어 각 노드에서는 단순히 입력 값들을 받아 연산해서 출력만 하면 된다. 이를 국소적 계산이라고 한다.
계산 그래프를 사용하면 역전파를 이해하기가 좀 더 쉽다.
위의 사과 예시에서 사과의 가격을 x, 지불 금액을 L이라고 하면 구해야 하는 값은 ∂L/∂x이다. 지불 값을 1로 두고 생각하면 다음의 계산 그래프와 같이 나타낼 수 있다.
연쇄 법칙
합성함수란 여러 함수로 구성된 함수이다. 예를 들어 다음의 z는 합성 함수로 나타낼 수 있다.
z = (x+y)^2
z = t^2
t = (x+y)
이러한 합성함수의 미분은 합성함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다. 위 z함수를 예시로 들면 다음과 같다.
∂z/∂x = ∂z/∂t * ∂t/∂x = 2t * 1 = 2(x+y)
이를 계산 그래프로 나타내면 다음과 같이 표현할 수 있다.
역전파
덧셈노드의 역전파는 계산 그래프를 사용하면 아래와 같이 나타낼 수 있다.
즉, 덧셈노드의 역전파는 사실상 받은 값을 그대로 넘겨주는 것이다.
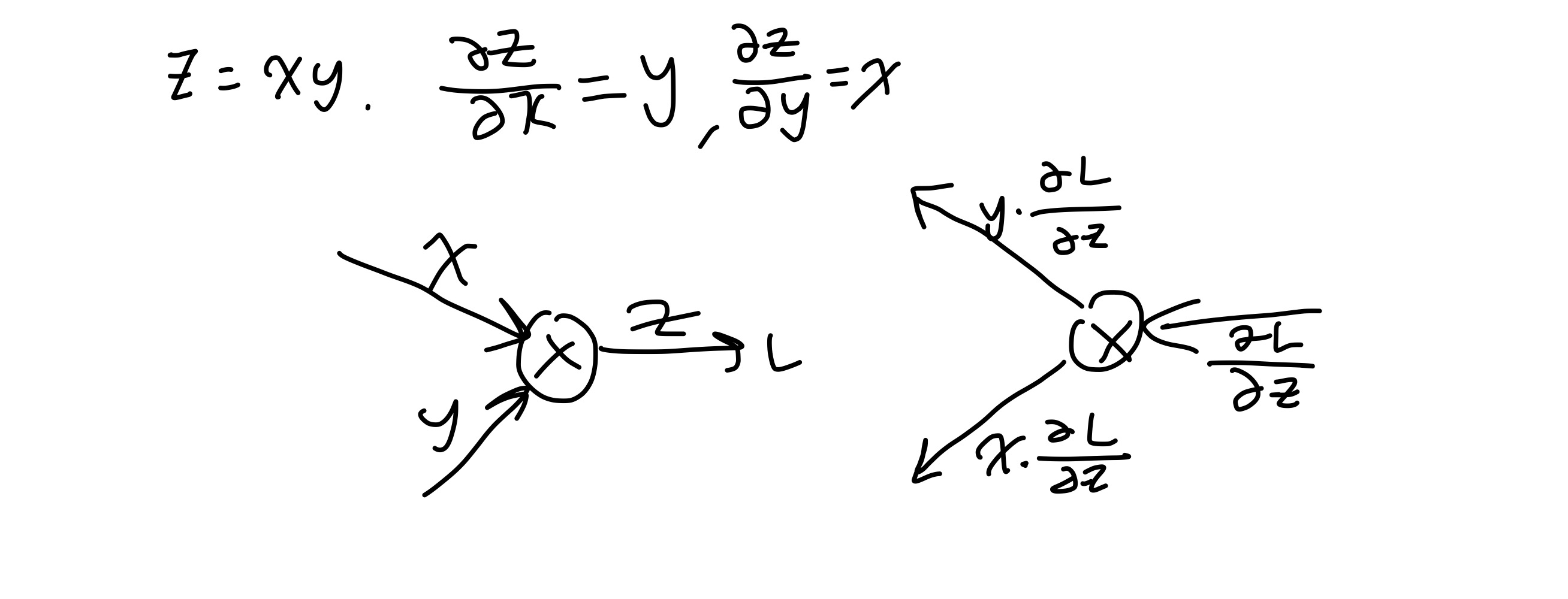
곱셈노드의 역전파는 계산 그래프를 사용하면 아래와 같이 나타낼 수 있다.
즉, 곱셈노드는 역전파시 입력신호를 서로 바꾼 값을 곱해 전파를 한다. 이 때 입력신호를 알아야 하기 때문에 구현 시 이를 따로 저장해둔다.
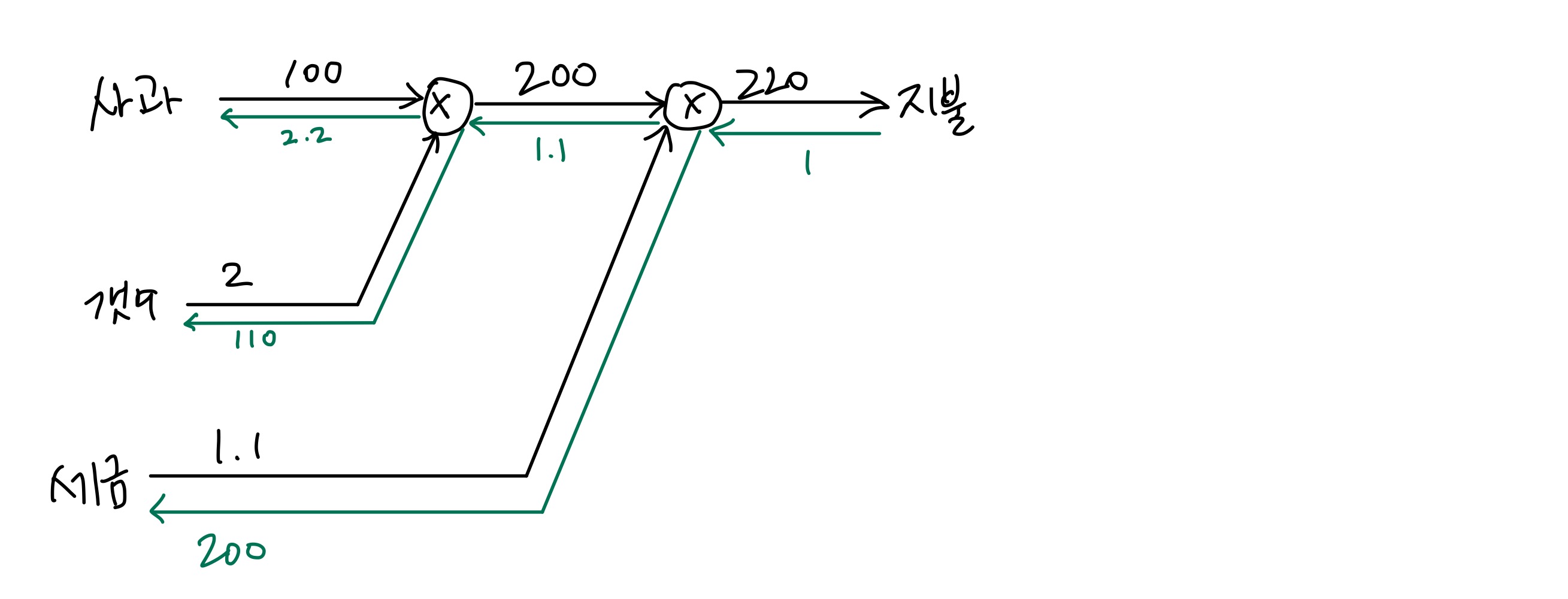
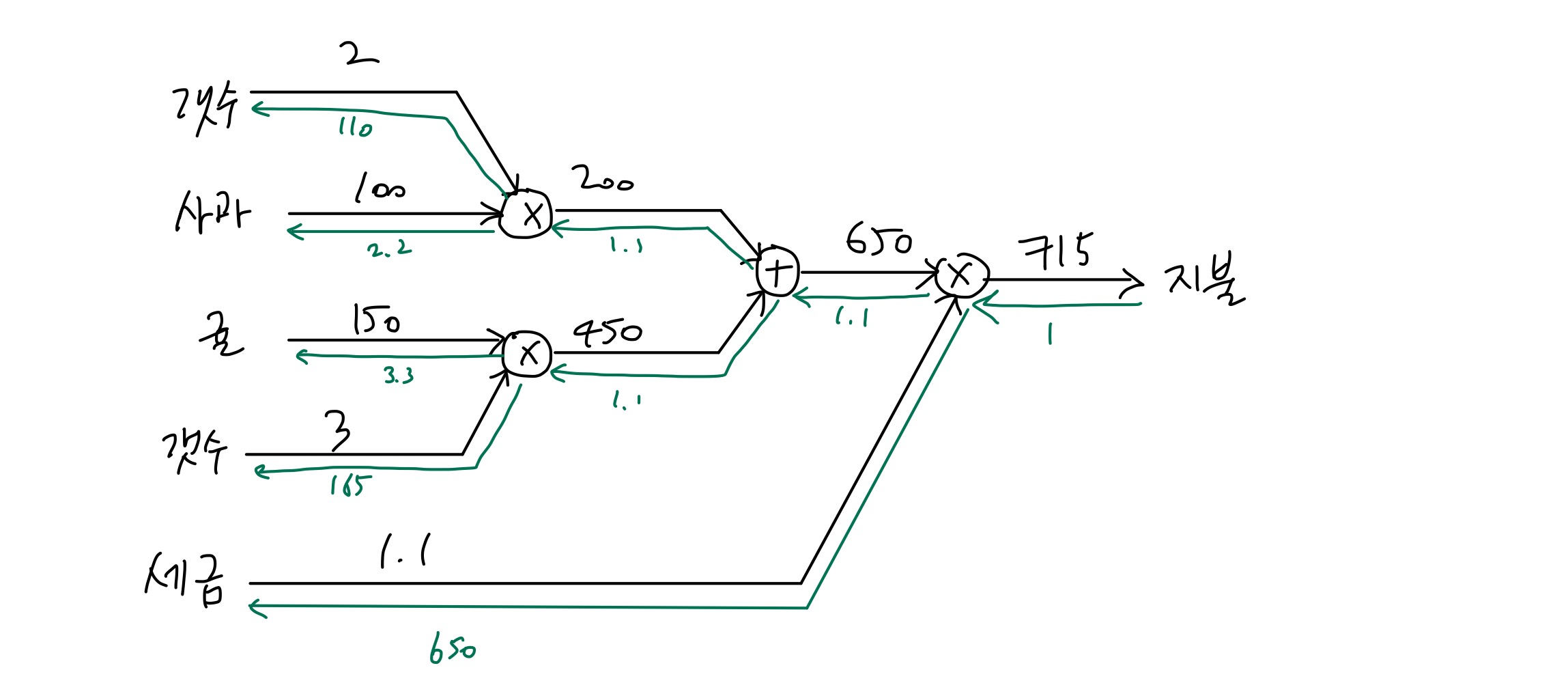
이해를 위해 아까의 사과 귤 구입 예제에 대한 역전파를 계산 그래프로 표현하면 아래와 같다.
구현 (계산그래프 위주로 설명, 코드는 깃헙에 업로드함)
이제 지금까지 배운 계층들을 구현해볼 단계이다.
계층은 기능의 단위인데 모든 계층은 forward()와 backward() 기능을 가지고 있다. 필요한 값은 저장을 해주는데 예를 들어 곱셈 노드에서는 입력받은 x와 y를 기억해야 하기 때문에 self.x, self.y에 각각 x, y값을 저장해준다.
활성화함수 중 ReLU 함수는 0보다 크면 그대로 출력하고 0보다 작거나 같으면 0을 출력해주는 함수인데 역전파에서는 0보다 크면 받은 값을 그대로 전파하고 0보다 작으면 0을 전파한다. 아래의 사진을 참고하면 될 것 같다.
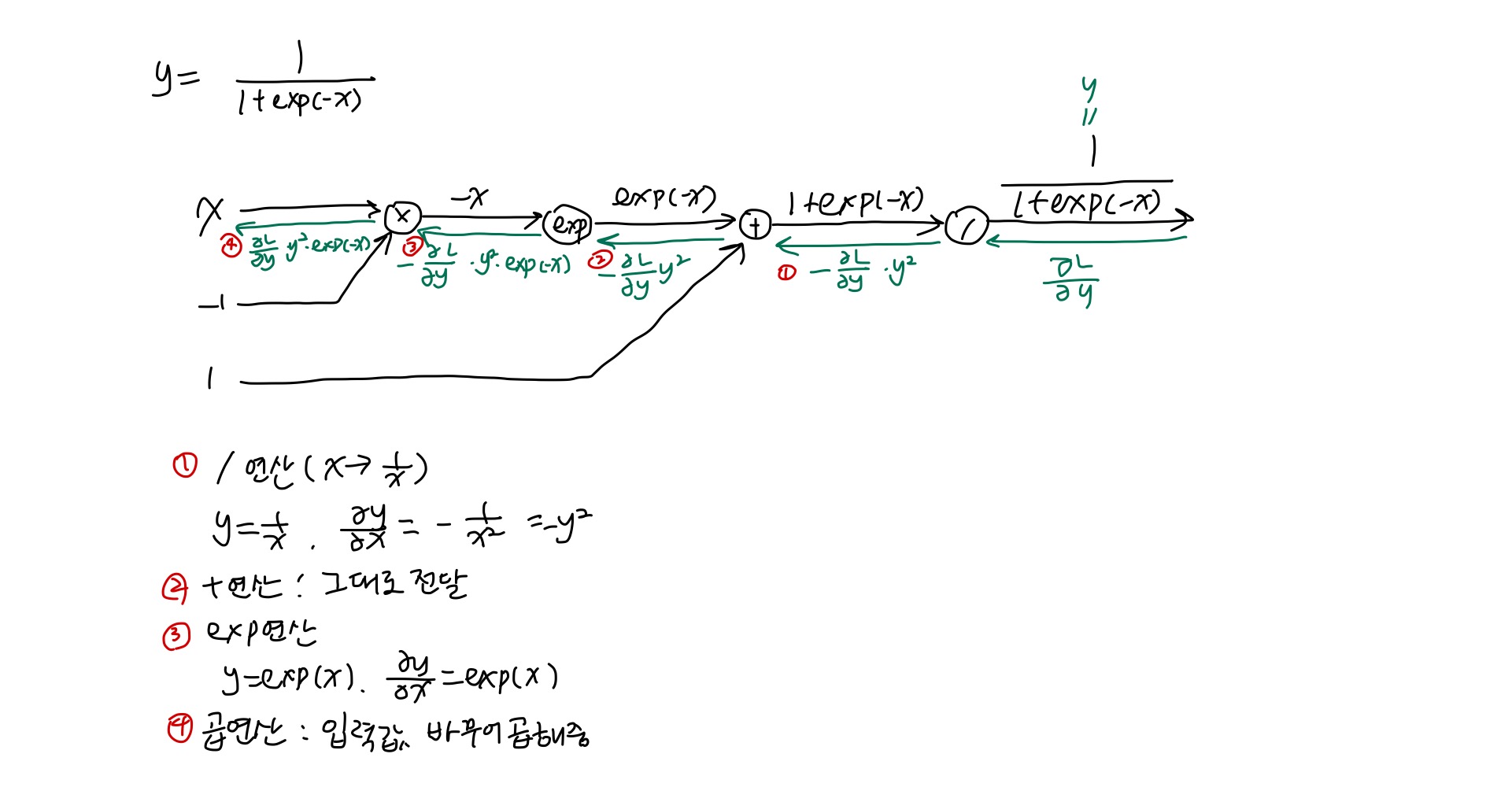
sigmoid 계층은 계산 그래프로 나타내면 아래와 같이 나타낼 수 있다. 역전파의 단계적 설명 또한 그림에서 같이 확인할 수 있다.
이 전체 과정을 하나의 sigmoid 노드로 묶으면 다음과 같이 표현할 수 있다.
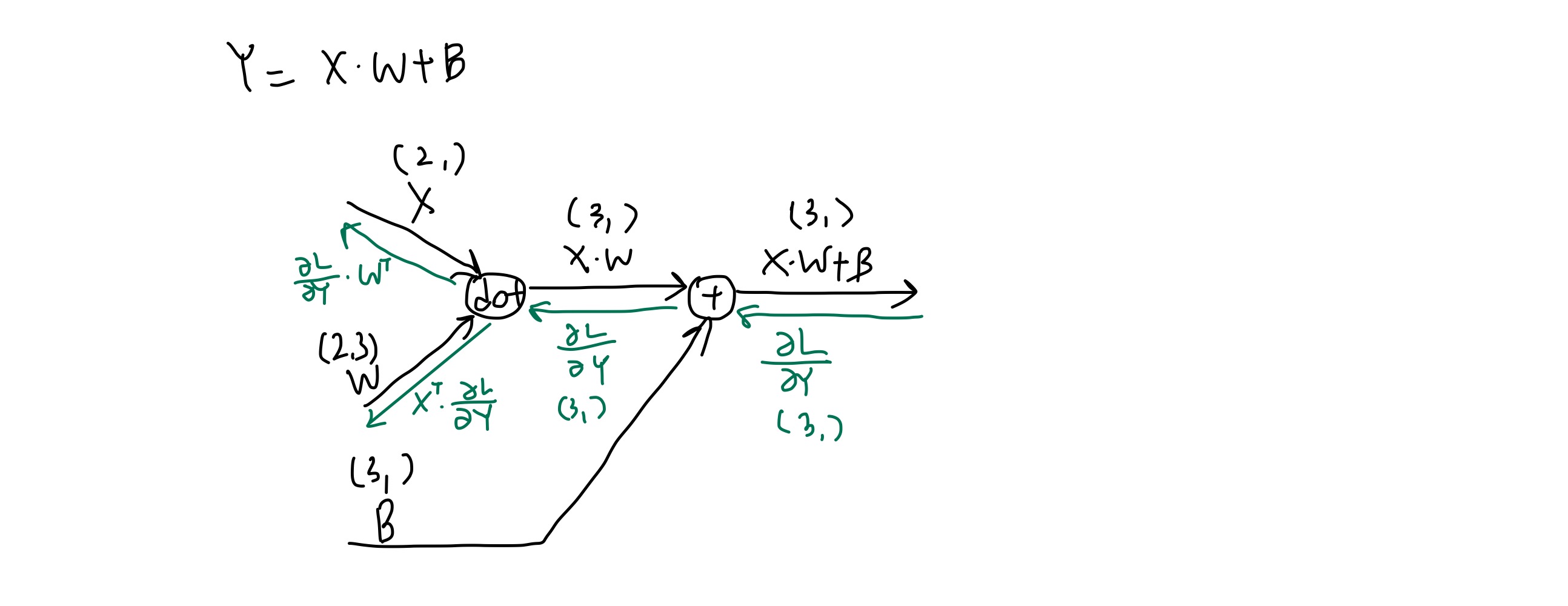
Affine 계층은 신경망의 순전파 과정에서 수행하는 행렬의 곱을 수행하는 계층이다. 계산 그래프로 나타내면 다음과 같다.
여기서 역전파가 왜 저렇게 되는지 유도과정이 책에 안나와있어서 언니의 머리를 빌려 이해를 해보았다.
softmax 함수는 각 레이블이 나올 확률을 계산해주는 기능을 하는데, 학습 시에 사용되고 추론 시에는 사용되지 않는다. 이 이유는 앞의 단원에 서술이 되어있는데 확률값으로 바꿔도 값들의 대소관계는 변하지 않기 때문이다.
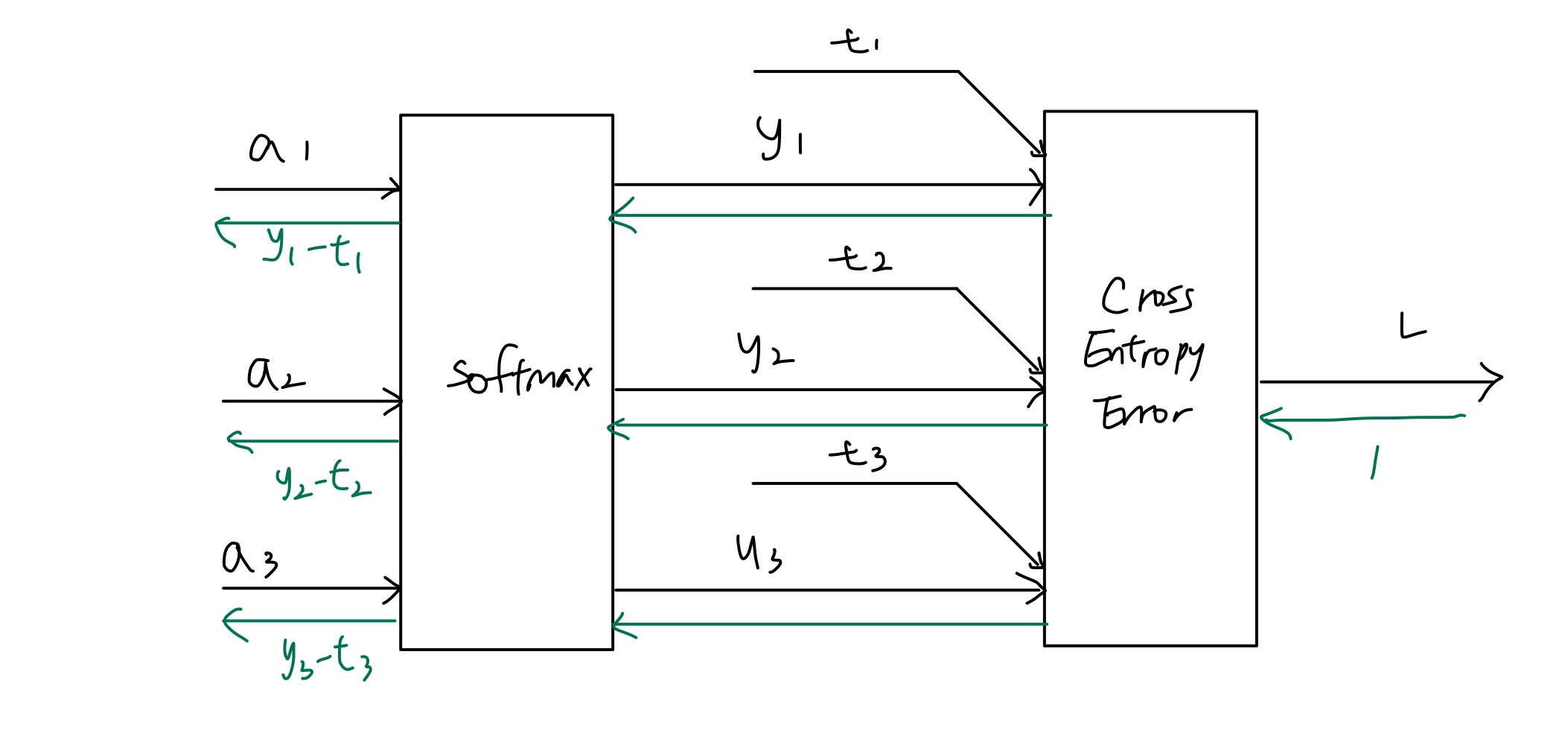
softmax 계층 구현 시에는 손실함수인 교차 엔트로피 오차도 포함하여 Softmax-with-loss 방식으로 구현을 한다. 이를 계산 그래프로 나타내면 다음과 같다.
이 softmax-with-loss 함수가 역전파시 전파하는 값은 의외로 매우 깔끔하다. 정답 레이블이 (t1, t2, t3)이고 예측 값이 (y1, y2, y3)일 때 역전파 값은 (y1-t1, y2-t2, y3-t3)으로 참값과 예측값의 차이 값인데, 사실 이는 교차엔트로피 함수를 만들 때 이러한 부분을 고려해서 만들어졌기 때문이라고 한다.
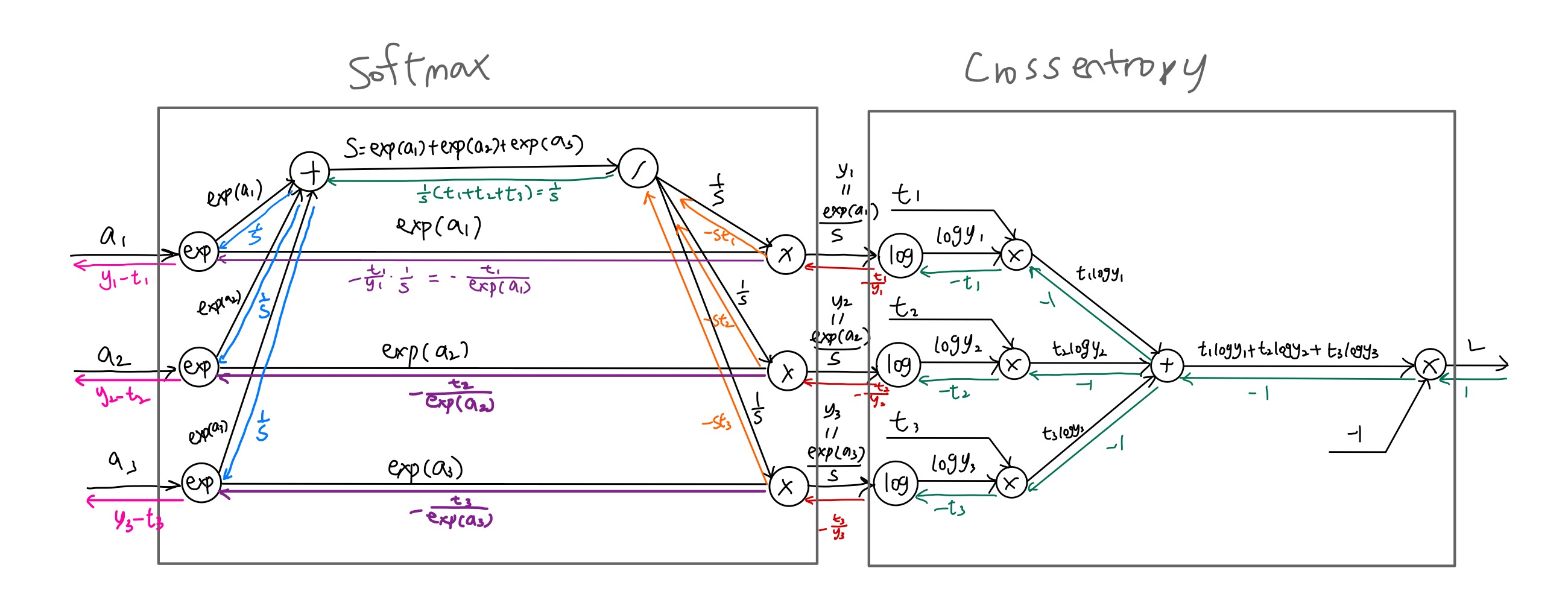
softmax-with-loss 함수의 순전파 및 역전파 전체 과정은 다음과 같다.
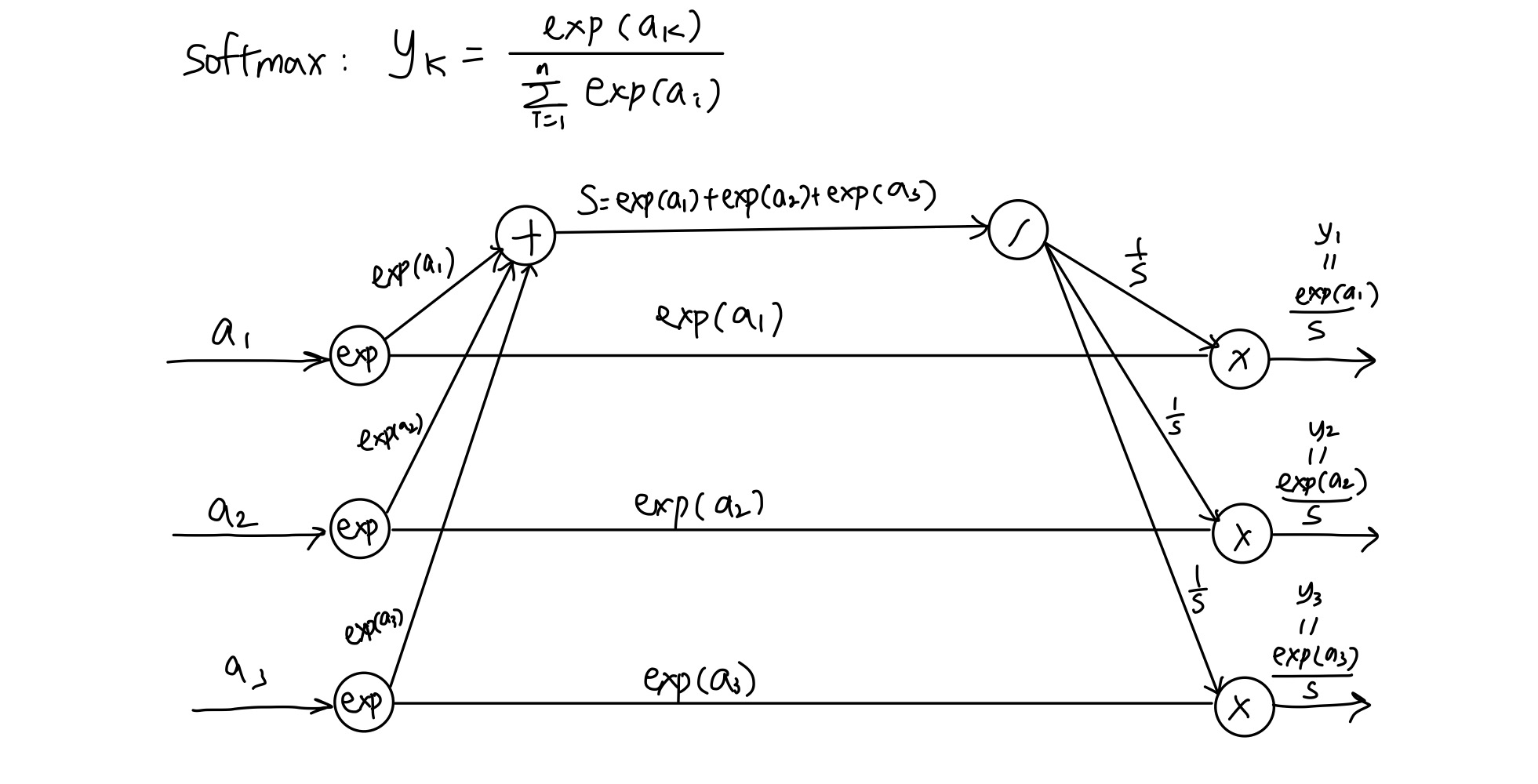
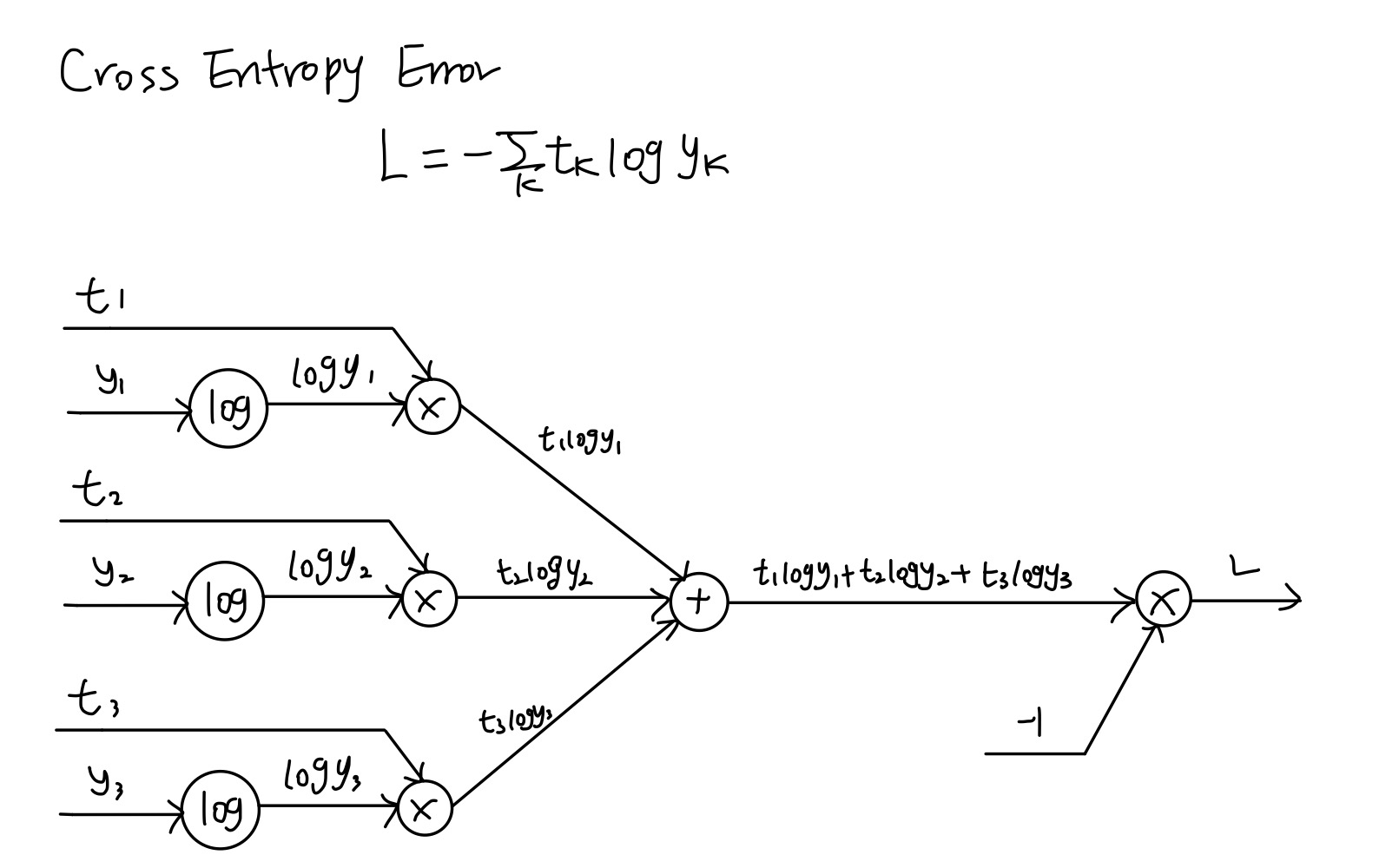
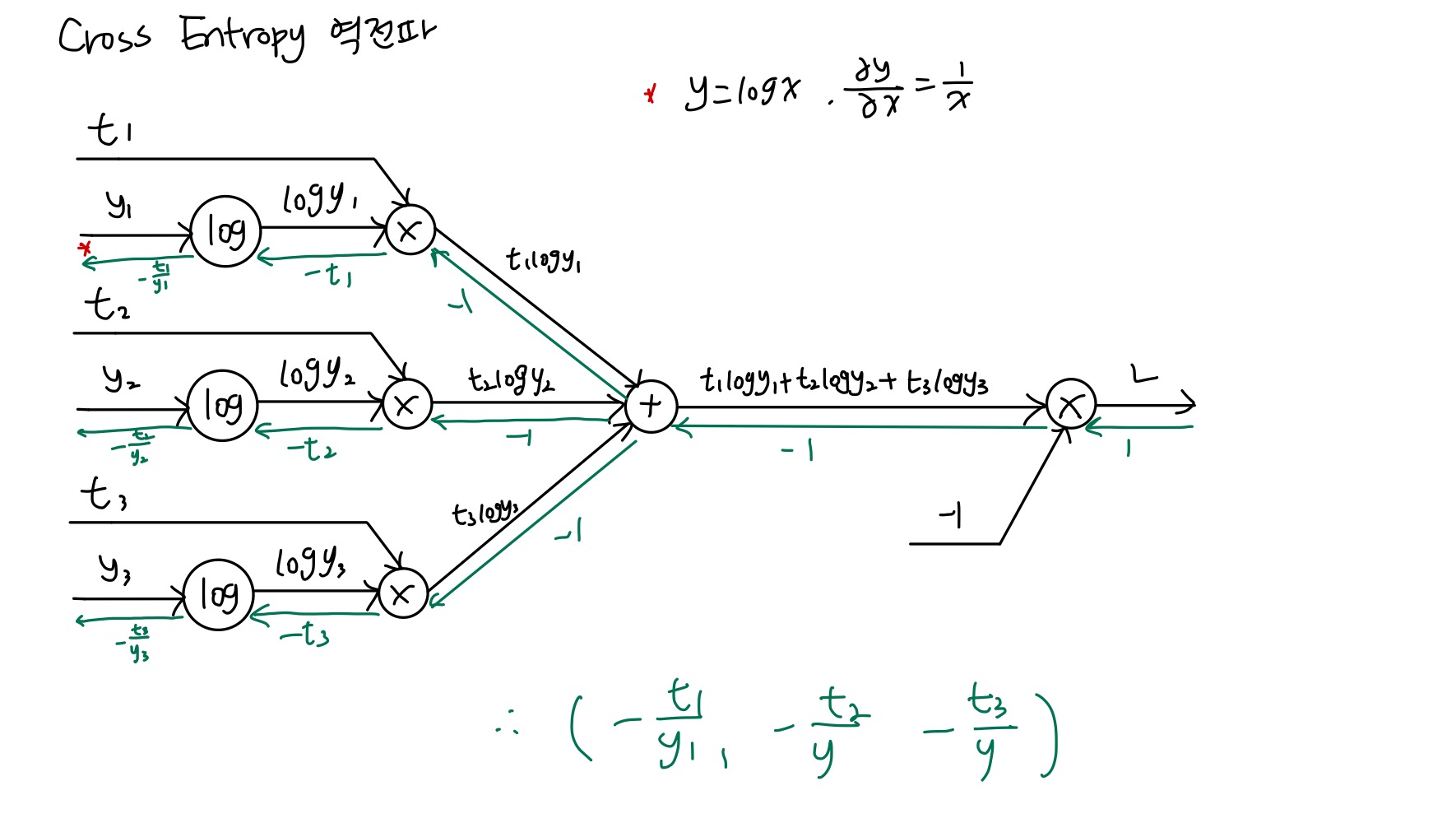
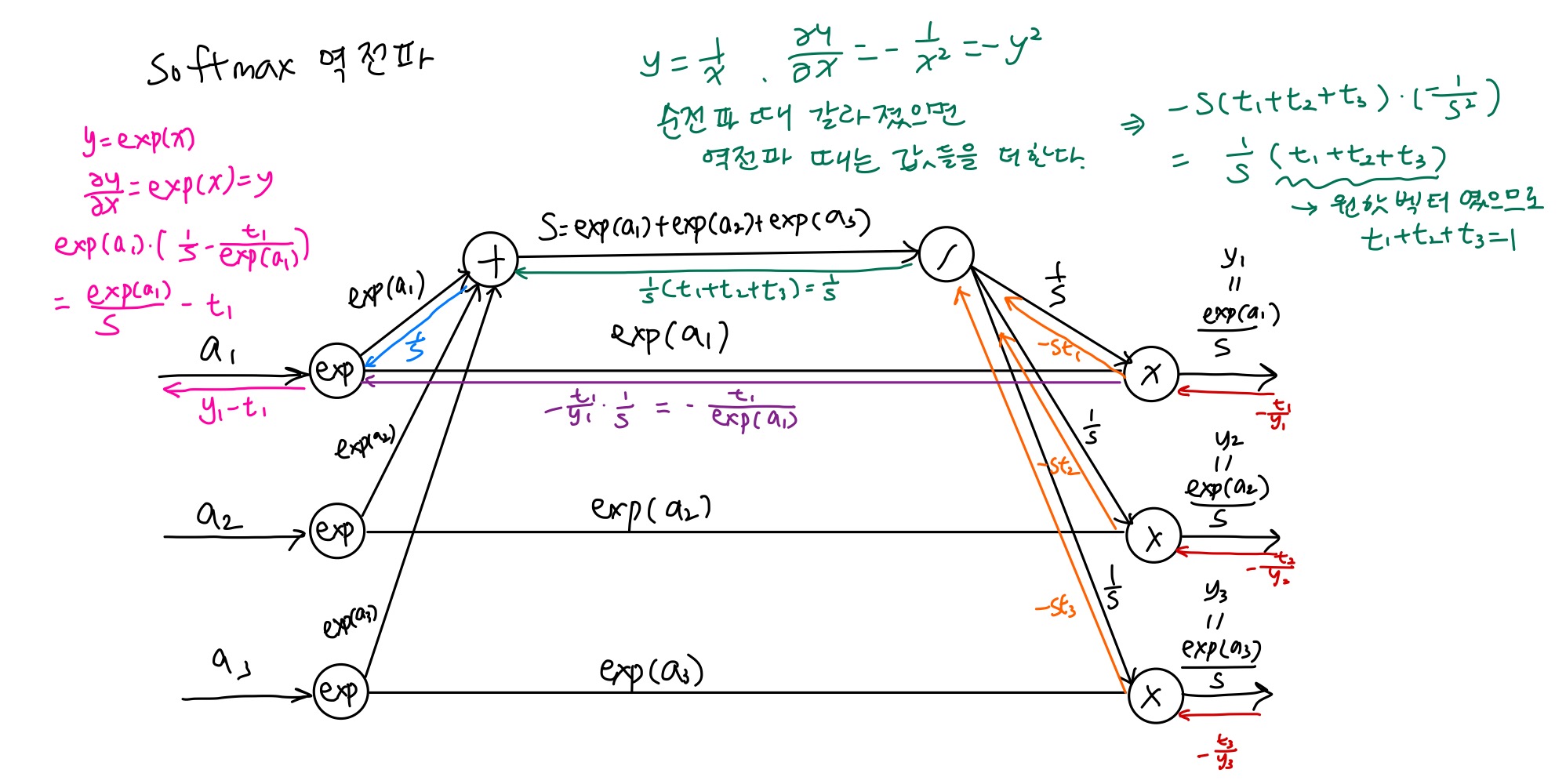
참고로 역전파 시에는 전파하는 값이 데이터 1개당 오차이기 때문에 배치를 사용할 때 배치의 크기로 나눠줘야 한다.
오차역전파법 구현
신경망에는 적용 가능한 가중치와 편향이 있고, 이 가중치와 편향을 조정하는 과정을 학습이라고 한다.
신경망 학습의 순서는 다음과 같다.
- 미니 배치: 훈련 데이터 중 일부를 무작위로 가져온다.
- 기울기 산출: 각 가중치 매개변수의 기울기를 구한다. 기울기는 손실함수의 값을 가장 작게 하는 방향을 제시한다.
- 매개변수 갱신: 가중치 매개변수를 기울기 방향에 따라 조금씩 갱신한다.
- 반복: 1~3 단계를 반복한다.
이 중 오차역전파법이 적용되는 단계는 2단계인 기울기 산출에 해당한다. 앞서 시도한 수치 미분과 달리 기울기를 효율적이고 빠르게 구할 수 있다.
구현은 OrderDict를 사용하여 계층을 켜켜이 쌓는다.
수치 미분은 오래 걸리는 대신 구현하기가 쉽고, 오차역전파법은 빠른 대신 복잡해서 구현시 실수를 할 가능성이 높은데, 그래서 두 방식으로 구한 기울기를 비교하는 것을 기울기 확인(gradient check)이라고 한다. 실제로 코드를 돌려보면 두 방식의 결과가 매우 유사하다는 것을 확인할 수 있다.
구현 코드는 link에서 확인할 수 있다.