3. 신경망

12 Nov 2020

신경망은 기본적으로 다음과 같이 생겼다.

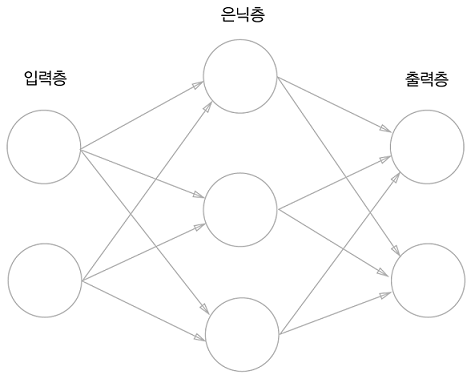
여기서 은닉층은 실제로는 보이지 않는다.

신경망에 대해 알아보기 전에 이전 단원에서 본 퍼셉트론을 떠올려 보자.

퍼셉트론에서는 b + w1x1 + w2x2가 0보다 작거나 같으면 0, 0보다 크면 1을 출력되게 했었는데, 이를 함수로 만들면 다음과 같이 표현할 수 있다.

y = h(b+w1x1+w2x2),
h(x) = 0 (x<=0), 1 (x>0)

이렇듯 입력 신호의 총 합을 출력신호로 변환해주는 함수를 일반적으로 활성화 함수(activation function)라고 부른다.

활성화 함수에는 여러가지 종류가 있는데, 그 중 퍼셉트론은 임계값을 경계로 출력이 바뀌는 계단함수를 사용한다. (사실 퍼셉트론과 신경망의 주된 차이점은 활성화 함수의 차이이다.)

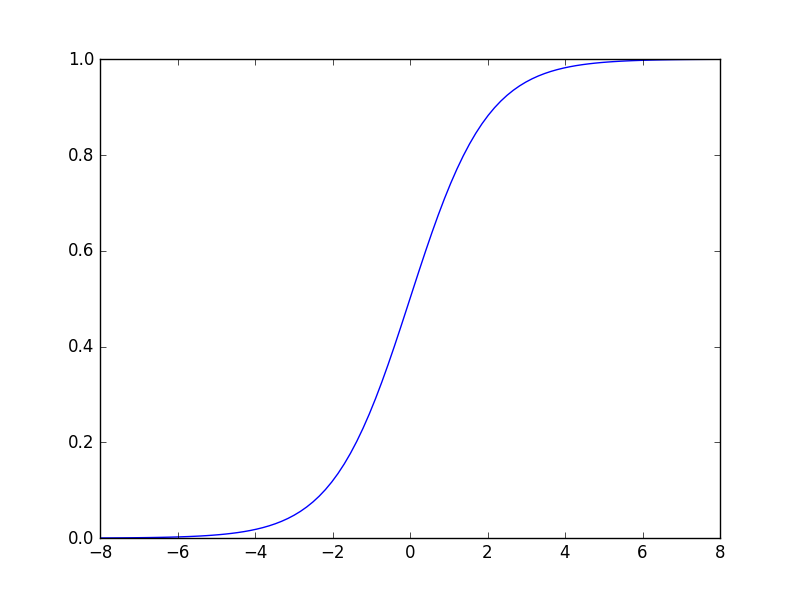
다른 활성화 함수로는 먼저 시그모이드(sigmoid) 함수가 있다. 시그모이드와 계단함수의 차이는 시그모이드는 부드러운 곡선이고 출력값으로 실수값도 나올 수 있지만 계단함수는 임계값을 기준으로 값이 확 바뀌고 출력이 0 또는 1로만 나온다는 점이다. 하지만 큰 틀에서는 입력이 작을때는 출력이 0에 가깝고 입력이 클 때에는 출력이 1에 가까워지는 구조이고, 둘 다 비선형 함수(선형이 아니다)라는 점에서 유사한 점도 있다.

선형 함수의 경우 신경망을 여러 층으로 쌓는 의미가 없기 때문에 활성화 함수로는 비선형 함수를 사용해야 한다.

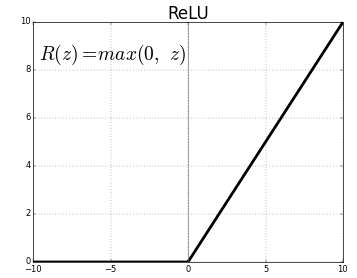
또 다른 활성화 함수로는 ReLU 함수가 있는데, ReLU함수는 입력이 0 이하이면 0을 출력하고 0보다 크면 입력값을 그대로 출력하는 함수이다.

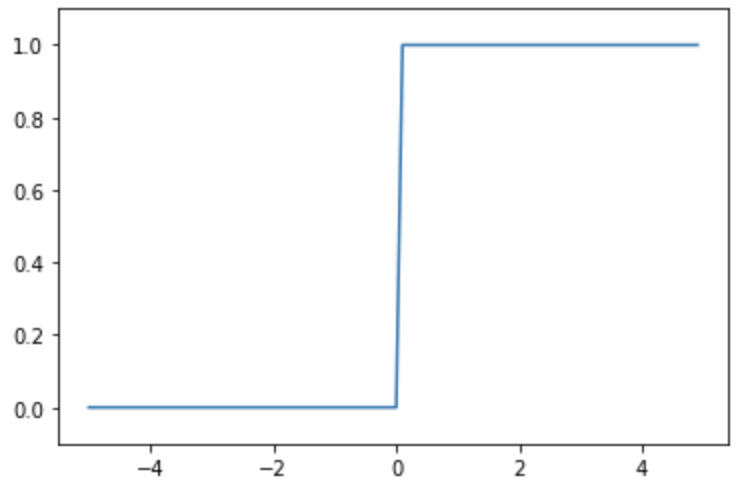
아래는 순서대로 계단함수, 시그모이드 함수, 그리고 ReLU함수이다.

이제 3계층 신경망에서 어떤 방식으로 순방향 학습이 이루어지는지를 코드와 함께 보도록 하자.

먼저 우리가 코드로 구현할 3계층 신경망은 다음과 같다.

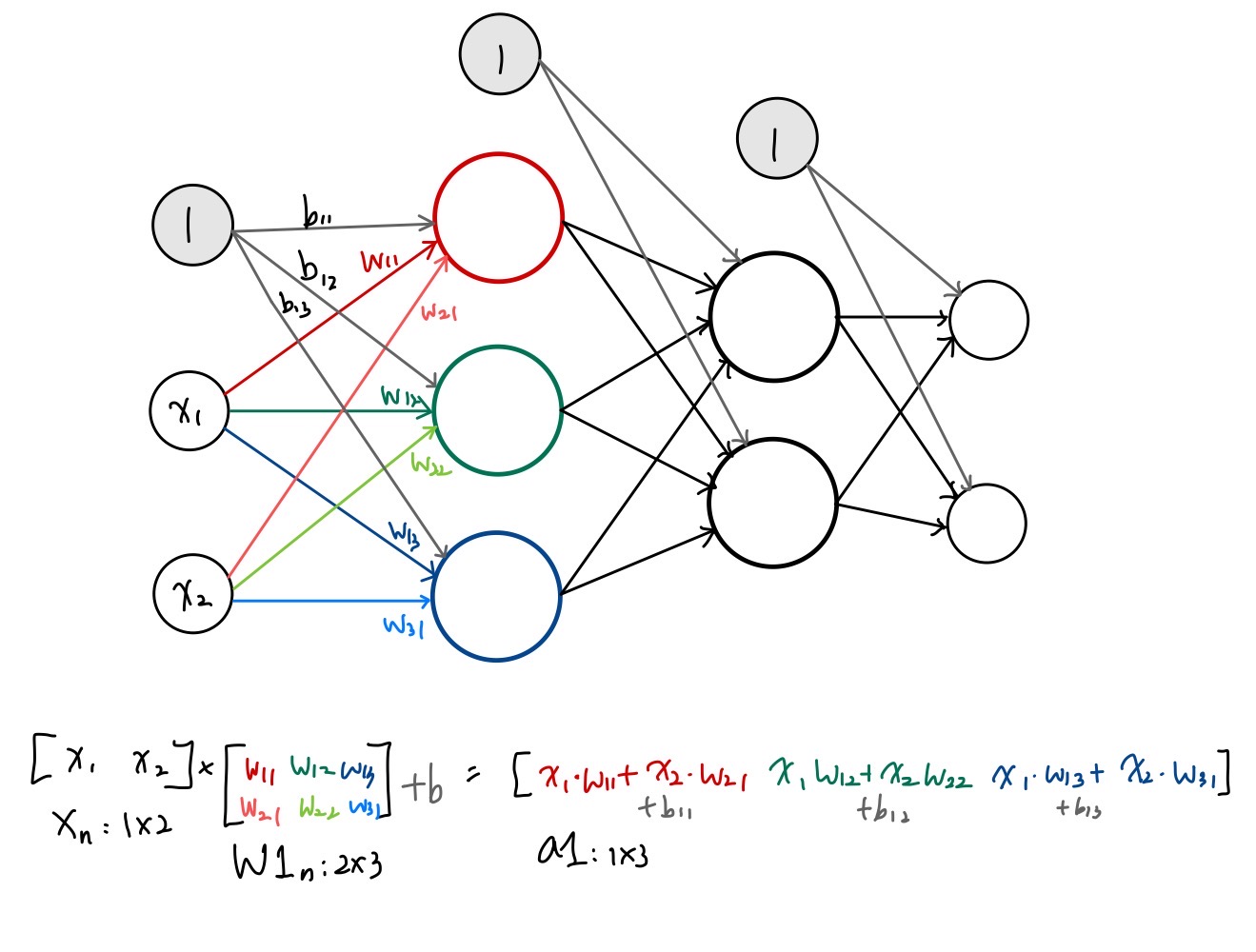
편의를 위해서 첫번째 계층에서의 연산만 표시를 해두었다. 그림과 같이 각 x값에 각각에 해당하는 가중치를 곱해서 더해주고 추가적으로 편향값을 더해주면 다음 은닉층의 입력값이 되는데, 여기서 활성화 함수를 적용해주면(코드의 경우 sigmoid 함수를 적용해주었다) 이것이 해당 은닉층의 출력값이자 다음 층의 입력값이 된다.

마지막 출력층의 경우 활성화 함수를 자기 자신을 출력하는 identity 함수를 사용하는데, 출력층의 활성화 함수는 뒤에서 마저 더 깊게 공부를 해보도록 할 것이다.

코드는 다음과 같다.

그럼 출력층에 대해 더 깊이 알아보도록 하자.

신경망의 출력층에서 어떤 활성화 함수를 쓰냐에 따라 해결할 수 있는 문제가 달라지는데, 예를 들어 항등 함수를 사용하면 회귀 문제를 해결할 수 있고, 소프트맥스 함수를 사용하면 분류 문제를 해결할 수 있다.

항등 함수는 앞서 본 identity 함수처럼 입력을 그대로 출력하는 함수를 말한다. Softmax 함수는 입력된 모든 값들 중 각각의 값이 나올 확률을 계산해주는 함수이다. 소프트맥스 함수를 사용할 때에는 고려해야 할 점이 있는데 지수 함수를 사용하기 때문에 컴퓨터로 계산할 때 오버플로우가 생기지 않게 주의해야 한다는 것이다.

위와 같이 softmax값을 계산하는 식을 잘 정리해보면, 각각의 ai값에 같은 값을 더하거나 빼줘도 결과값은 동일하다는 것을 알 수 있다. 이 특징을 활용해서 각 ai에서 최댓값을 빼주면 오버플로우를 방지할 수 있다.

softmax 함수의 특징으로는 출력값이 0과 1 사이의 실수이고, 모든 출력의 총합이 1이라는 것이다. 이 성질을 활용하여 softmax 함수의 출력을 확률값으로 해석할 수 있다.

하지만 softmax를 적용한다고 해서 softmax를 사용하기 전의 값들의 대소관계는 변하지 않기 때문에(지수함수가 단조 증가 함수이기 때문) 현업에서는 학습시에는 출력층에서 softmax를 사용하고, 추론시에는 출력층의 softmax 함수를 생략하는 경우도 매우 많다고 한다.

출력 층의 뉴런의 개수는 풀려는 문제에서 분류하고 싶은 클래스의 개수로 주로 설정한다.

배치 처리란 여러개의 데이터를 한 번에 묶어서 연산을 하는 방식을 말하는데, 적절한 개수의 데이터를 하나의 배치로 묶어서 학습을 시키면 하나씩 연산하는 것보다 훨씬 효율적이고 빠르게 데이터를 처리할 수 있다.